データ分析
導入
分析結果は分析時点での入力データに基づくものであり、入力データを修正しても分析結果は更新されません。
分析ツールの有効化
分析ツールはアドインとして提供されており、既定では有効になっていません。
これを有効にするには、Officeボタンから[Excelのオプション]、そして[アドイン]のページを開きます。さらに管理ボックスで[Excelアドイン]を選択し、[設定]をクリックします。そして開かれたダイアログボックスで[分析ツール]にチェックを入れ、[OK]をクリックします。分析ツールを読み込む - Office のサポート
分析ツール利用時に「'ANALYS32.XLL' にアクセスできません。ファイルが破損しているか、応答しないサーバーにあるか、読み取り専用に設定されています。」としてエラーとなるときには、%PROGRAMFILES(X86)%\Microsoft Office\Office12\Library\Analysis\ANALYS32.XLLにある、このファイルを確認します。
起動
[データ]タブの[分析]グループにある、[データ分析]から起動できます。
機能
| 種類 | 用途 |
|---|---|
| 分散分析: 一元配置 | 複数の標本データの分散の簡単な分析 |
| 分散分析: 繰り返しのある二元配置 | データを2つの異なる次元で分類 |
| 分散分析: 繰り返しのない二元配置 | |
| 相関 | |
| 共分散 | |
| 基本統計量 | |
| 指数平滑 | |
| F 検定: 2 標本を使った分散の検定 | |
| フーリエ解析 | |
| ヒストグラム | |
| 移動平均 | |
| 乱数発生 | |
| 順位と百分位数 | |
| 回帰分析 | |
| サンプリング | |
| t 検定: 一対の標本による平均の検定 | |
| t 検定: 等分散を仮定した 2 標本による検定 | |
| t 検定: 分散が等しくないと仮定した 2 標本による検定 | |
| z 検定: 2標本による平均の検定 |
基本統計量 (Descriptive Statistics)
既定では統計情報のみが出力されます。それ以外の項目を出力するには、[出力オプション]にある項目にチェックを入れます。
| オプションの項目 | 出力項目 |
|---|---|
| 統計情報 | 他の項目以外 |
| 平均の信頼区間の出力 | 信頼区間 |
| K 番目に大きな値 | 最大値 |
| K 番目に小さな値 | 最小値 |
| 出力項目 | 対応する関数 | 説明 |
|---|---|---|
| 平均 (Mean) |
AVERAGE(データ範囲) | |
| 標準誤差 (Standard Error) |
STDEV(データ範囲)/SQRT(標本数) | |
| 中央値 (メジアン) (Median) |
MEDIAN(データ範囲) | |
| 最頻値 (モード) (Mode) |
MODE(データ範囲) | |
| 標準偏差 (Standard Deviation) |
STDEV(データ範囲) | 標準偏差とは、統計的な対象となる値がその平均からどれだけ広い範囲に分布しているかを表すもの
(実際は標本標準偏差) |
| 分散 (Sample Variance) |
VAR(データ範囲) |
(実際は不偏分散) |
| 尖度 (Kurtosis) |
KURT(データ範囲) | 尖度とは、対象となるデータの分布を標準分布と比較して、度数分布曲線の相対的な鋭角度または平坦度を数値で表すもの。分布を図示したときの、中心部分の尖り具合
|
| 歪度 (Skewness) |
SKEW(データ範囲) | 歪度とは、分布の非対称性の方向、及びその程度を表すもの。分布を図示したときの、左右の歪み具合
|
| 範囲 (Range) |
MAX(データ範囲)-MIN(データ範囲) | |
| 最小 (Minimum) |
MIN(データ範囲) | |
| 最大 (Maximum) |
MAX(データ範囲) | |
| 合計 (Sum) |
SUM(データ範囲) | |
| 標本数 (Count) |
COUNT(データ範囲) | |
| 最大値(k) | LARGE(データ範囲,k番目) | |
| 最小値(k) | SMALL(データ範囲,k番目) | |
| 信頼区間 (Confidence Level) |
CONFIDENCE(有意水準,標準偏差,標本数) (信頼度が95%ならば、有意水準は(100-95)/100で0.05とする) |
信頼区間とは、ある母集団の100(1-α)%のデータが平均値から見てどのくらいの開きのある範囲 (計算結果は平均値から見た片側の範囲) に存在するかを考えたときの、その範囲。αは有意水準 (危険率) |
≫統計関数
フーリエ解析 (Fourier Analysis)
高速フーリエ変換 (FFT) で分析されます。データは2の偶数乗個である必要があり、最大は4096個です。
ヒストグラム (Histogram)
たとえば下表のデータがあるとき、
| A | B | |
|---|---|---|
| 1 | 30 | 10 |
| 2 | 25 | 20 |
| 3 | 10 | 30 |
| 4 | 20 | |
| 5 | 25 | |
| 6 | 35 | |
| 7 | 15 |
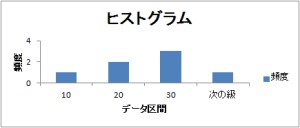
入力範囲を「$A$1:$A$7」、データ区間を「$B$1:$B$3」とすると、
| データ区間 | 頻度 |
|---|---|
| 10 | 1 |
| 20 | 2 |
| 30 | 3 |
| 次の級 | 1 |
のように結果が出力されます。そのとき[グラフ作成]にチェックを入れておくと、下図のように出力されます。
同様の結果を関数で得るには、縦に4つのセルを選択した状態で=FREQUENCY(A1:A7,B1:B3)と入力し、Ctrl + Shift + Enterで配列数式とします。森本家のワークシート - ヒストグラムを一発で:ITpro 森本篤徳 (2007/08/29)